Develop mathematical model of age of water and carbon
Contents
Concept
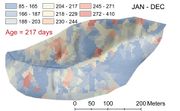
From the physical science perspective the research focuses on theoretical and experimental aspects of the isotopic “age” of water in lake-catchment systems. In this context, “age” is defined as the time since the water parcel and environmental tracer entered the system as precipitation. We note that each of our communities have developed an observing system for isotope ratios of carbon, oxygen and hydrogen but with very different science questions. In this research we will test a framework using models and data for defining a unified “isoscape” for the watershed-lake system, forming a richer and more collaborative shared research strategy. Our hypothesis is that the lake-catchment isoscape provides the experimental basis for predicting flow paths, residence times and the relative age of water in space and time, and that understanding these spatiotemporal patterns will provide a deeper understanding of fundamental biogeochemical processes including carbon and nitrogen cycling within the lake-catchment system. There is a wide literature on the use of residence time and relative age distribution of isotopes in environmental systems. Theories have been proposed using tracers for age modeling in ocean ventilation, atmospheric circulation, soil water, stream, groundwater flow, biophysics of vegetation photosynthesis as well as the circulation of blood. We begin this research with a simple model for the age of an environmental tracers in a ecohydrologic setting. Details of the approach can be found in Duffy (2010). The figure below is a simulation for the space-time distribution of isotopic age from the Shale Hills Critical Zone Observatory (Bhatt, 2012).
A useful analogy to understand the concept of “age” comes from population biology (Forester, 1959; Rotenberg, 1972). Consider a random population of individuals (species or particles) being born, dying and migrating. Given a long-term census of the population, the distribution of the size of the population through time and the distribution of ages of the population through time can be evaluated. Other moments may also be useful and can easily be determined from the census given enough data. The important concept to consider here is that there are actually two things we wish to evaluate in our long-term census: the number of individuals in our population through time, and the mean age of the population through time. For dissolved chemical species in water each component is characterized by physical time (clock time) and by the relative time or age since the species entered the system. The relative time for each component has it's own frame of reference particular to the dynamics of the flow system, the transport processes and the interaction with other components in the system.
In the context of the present study, our goal is to construct a statistical census for the isotopes of water and carbon or other nutrients in a lake-catchment system, that allow a mapping of the time evolution and the ageing of the complex physical, chemical and biological pathways of the modeled system.
A Well-Mixed Lake
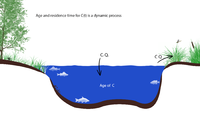
We begin with a simple lake or reservoir model for a single input and output as shown in Fig. 2. We define the isotopic “age” as the elapsed time since the particular isotope has entered the system as input. In other words the isotope sample is assumed to have zero age upon entering the lake. We note that in general, the isotopic age is a statistical quantity that depends on the sources of tracer, the particular transport and flow processes, the biochemical interactions, as well as the boundaries and initial conditions of the physical system. Over the course of this project we will demonstrate the concept of “age” for a fully-coupled, spatially-distributed, lake-catchment system. In this basic example we demonstrate how the age of the tracer is a simple extension of traditional ecohydrologic models.
Figure 1 illustrates the conceptual model for this example. A field experiment would involve sampling the lake input, storage volume and outlet for flow rate and isotope values over some time interval. Each sample that enters the lake has two properties: the particle mass m and the time since the mass entered the system. For particles entering the system randomly, the joint distribution function or probability density function for concentration of the tracer in the lake is given by the function , which describes the number of particles in the lake volume for time interval and age interval.In general, the functional form of c(t,Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \tau ) is required to develop complete information on the joint age-time distribution for our experiment, and this might be accomplished by fitting a particular function to experimental data. Although it is straight-forward to estimate the mass of our tracer in each sample volume, it is not generally feasible to determine the age of each sample. An alternative strategy is to relax the need for a colmplete description of the isotope population distribution and settle for a partial answer. That is, we assume c(t,Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \tau ) exists but with an unknown functional form, and with certain constraints on the moments. The usual rules of probability apply and we can estimate the moments in t by integrating c(t,Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \tau ) w/re to Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \tau (see Delhez, 1999 or Duffy, 2010):
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \operatorname{\mu_n}(t) = \int_0^{\infty} \tau^{n}c(t,\tau)\,d\tau,\quad n=0,1,2...\quad (1)
The 0th and 1st moment of (1) are given by:
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \mathit{C}(t)=\operatorname{\mu_0}(t) = \int_0^{\infty} \tau^{0}c(t,\tau)\,d\tau,\quad n=0;\quad (2)
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \mathit{A}(t)=\operatorname{\mu_1}(t) =\int_0^{\infty} \tau^{1}c(t,\tau)\,d\tau,\quad n=1;\quad (3)
where we identify the 0th moment as the tracer concentration C(t) and A(t) the 1st moment of c(t,Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \tau ). The key to our analysis is that the ratio of the 1st to 0th moment is the classical definition of the mean age of the system :
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \mathit{Age}= {\alpha}(t) = \frac{\mu_1}{\mu_0} \ =\frac{\mathit{A}(t)}{\mathit{C}(t)}\, \quad (4)
However, now we have defined it as a dynamic variable rather than the constant or steady-state value usually considered. Equations (1-3) define the moment relations for our experiment, and the next step is to develop a mathematical model for the physical system based on these moments.
For a single input and output, the volumetric inflow rate is Qi [L^3/T]), the outflow is Q [L^3/T] and for simplicity the flow is initially assumed to be steady-state (Qi =Q). The input tracer Ci can be isotopes of water (Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \delta^{18} O
or Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \delta^{2} H
), carbon or other solutes. As was the case in the population example given earlier, we expect the mass balance for our system to be conserved w/re to both time and age, and this is represented in the model as:
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{\partial c}{\partial t}+\frac{\partial c}{\partial \tau}=\Gamma_c-\mathit{L}(c),\quad (5)
where the left hand side is the total derivative for time and age of the isotope, and the right hand side represents tracer inputs, transformations and outputs. Integrating (4) w/re to as in (1), and applying the moment equations (2) yields the following dynamical system for the first 2 moments {n=0,1}:
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{\partial C}{\partial t}=k\left ( \mathit{C_i} - \mathit{C} \right )
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{\partial A}{\partial t}=\left ( \mathit{C}- k\mathit{A} \right )\qquad (6)
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \mathit{Age}= {\alpha}(t) =\frac{\mathit{A}(t)}{\mathit{C}(t)},\quad
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\alpha}(\infty) =\frac{V}{Q} \ =\frac{\mathit{A}(\infty)}{\mathit{C}(\infty)}\,
where C(t) is tracer concentration, A(t) is the 1st moment, and their ratio is the the age Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \alpha (t) and Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \alpha (\infty) is the steady-state age of the lake, with input Ci . It should be noted that for a well-mixed reservoir, the steady-state age of the tracer is identical to the mean age of the tracer leaving the system (e.g. the steady-state residence time). Equation (6) shows that the age and residence time are actually dynamic quantities, with a constant asymptotic- or long-term average value. The asymptotic value is the traditional steady-state residence time.
The system (6) admits a closed form solution for steady flow conditions (Qi =Q), with constant input (Ci) and uniform initial conditions (C(0)=C0):
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \mathit{C}(t)=e^{-kt}\left ( \ \mathit{C_0}- \mathit{C_i}+ \mathit{C_i}e^{kt}\right )\,Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \mathit{A}(t)=\frac{e^{-kt}}{k}\left ( \ \mathit{C_i}e^{kt}- \mathit{C_i}+ \mathit{C_0}kt-\mathit{C_i}kt\right )\, \quad (7)
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \alpha(t)=\frac{\left ( \ \mathit{C_i}e^{kt}- \mathit{C_i}+ \mathit{C_0}kt- \mathit{C_i}kt\right )}{k\left ( \mathit{C_0}- \mathit{C_i}+ \mathit{C_i}e^{kt}\right )}\,
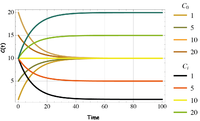
For purpose of discussion, Fig. 3 illustrates the tracer concentration solution trajectories for a range of initial conditions and inputs. Figure 4 illustrates the solution for the mean age of the tracer in the lake. It is important to realize that tracer age in the dynamical model is a relative quantity that also depends on the initial conditions and asymptotic “age” of the system at steady-state. In this case we assume the initial tracer age in the lake is α(t)=0 and the inputs Ci are zero age as they enter the lake (e.g. a birth in the population context). Of course other initial and input conditions are possible. Note that as
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): Q\Rightarrow 0\quad and Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): C_i\Rightarrow 0\quad , the system simply ages in clock time or the solution (7) is Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \alpha= t .
Case 1: Variable V/Q
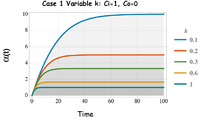
The solutions for in Fig. 4 shows the impact of varying the rate constant k (or steady-state age α( )=k-1) when the input concentration exceeds the initial condition, Ci. ≥ C0. The dynamic age of the tracer evolves from zero age to the asymptotic steady-state value. We see that the average age of the tracer in the lake and, by the well-mixed assumption, the age of the tracer in the outflow, will reach a constant age.
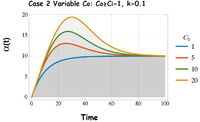
Case 2: Variable Initial Condition Co
The solutions for in Fig. 5 demonstrates that age calculations in models must be thought of as “relative age”, or the age since the start of the experiment. The initial condition C0 in Fig. 5 is varied while holding the input value at Ci=1. Note that when C0 > Ci, the early time age (t<V/Q) grows until the older water is displaced. The greater the concentration difference (C0 - Ci), the greater the effect on early time age. At late time in the event, the age solution gradually approaches the asymptotic age Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \alpha (t) . Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \alpha (\infty) .
In the catchment hydrology literature there has been a long- standing discussion about how to interpret the age of runoff. Typically, experiments find that old water or pre-event water chemical signatures dominate the runoff response during and after rainfall events (e.g. the runoff event concentration is much different than the precipitation concentration. It would seem that this simple experiment (case 2) explains why field observations of old water following an input event can be explained as a simple function of two conditions: the difference between the initial and input concentrations (C0 - Ci), and the steady-state age V/Q of the system.
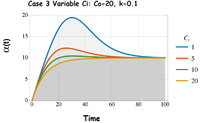
Case 3: Variable Input Ci
In case 3 (Fig. 6) the input for the tracer was varied, for a constant initial concentration (C0 =20). Again note that the early time age is depends on the difference (C0 - Ci) and the steady-state age is V/Q=10 years.
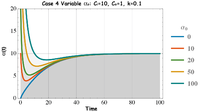
Case 4: Variable Initial Age α(0)
In cases 1-3, the initial condition for tracer age in the lake was assumed to be Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \alpha (0)=0 . In Case 4 we examine the effect of varying the initial age of the lake water and the solutions are given in Fig. 7. In systems where the initial age is old relative to the characteristic time of our system, the initially old water evolves to the new steady-state age in approximately 3 characteristic time scales, t~3V/Q. This example could be applied to the problem of assessing the impact of management practices, where contaminant inputs have been reduced and the time it takes to see the impacts on the lake or lake outflow is of interest. Performance assessment from reduced nutrient loading from agricultural runoff, or reduced atmospheric pollutants from the energy production and atmospheric contaminants, could apply a dynamic ageing model to assess the time it might take to measure the value of management practices and time to ecosystem recovery.
Transient Flow
We can extend the lake model to include transient flow. Following the same strategy as before the equations for flow and concentration have the form:
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{\partial \mathit{V}}{\partial t}= \left ( \mathit{Q_i} - \mathit{Q}\right )
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{\partial \left ( \mathit{VC}\right )}{\partial t}= \mathit{Q_i}\mathit{C_i} - \mathit{Q}\mathit{C}
where Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): Q_i is the lake input flux, Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): Q is lake outflow. Note that it is straight forward to include multiple input loadings Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): Q_i C_i, i=1,2,...n\quad . Expanding the 2nd equation and after some manipulation we arrive at our dynamical system for transient flow, tracer concentration and age for the lake assuming time variable storage-outflow:
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{\partial \mathit{V}}{\partial t}= \left (\mathit{Q_i} - \mathit{Q} \right )
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{\partial \mathit{C}}{\partial t}= \frac {1}{\tau_c} \left (\mathit{C_i} - \mathit{C} \right )
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{\partial A}{\partial t}=\mathit{C}- \frac {1}{\tau_c}\mathit{A} \qquad (7)
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \mathit{Age}= {\alpha}(t) =\frac{\mathit{A}(t)}{\mathit{C}(t)},\quad
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\tau_c}(t) =\frac{V(t)}{Q(t)}
where V(t) is the time variable lake volume, C(t) is concentration and A(t) is 1st moment. The characteristic time in this case is not constant Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\tau_c}(t) and the equations are nonlinear which will require numerical solutions.
Two-Zone Lake Model with Incomplete Mixing
Next we develop a two-zone model with incomplete vertical mixing as shown in Fig. ?? Diffusion is allowed between the well-mixed layers while advection occurs only in the surface layer. The equations for flow and concentration have the form:
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{\partial \mathit{V_1}}{\partial t}= \left ( \mathit{Q_i} - \mathit{Q}\right )
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{\partial \mathit{V_1 C_1}}{\partial t}= \mathit{Q_i}\mathit{C_i} - \mathit{Q}\mathit{C} +E'\left ( C_2 -C_1\right )
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{\partial \mathit{V_2 C_2}}{\partial t}= -E'\left ( C_2 -C_1\right )
where Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): Q_i is the net lake input flux, Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): Q_1 is lake outflow, Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): V_1 and Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): V_2 are the volumes of the surface and deep layers and Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): E' is a bulk diffusion coefficient. In this case we include multiple observed inputs:
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \mathit{Q_i}= Q_{in}+A_s P+A_s ET
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \mathit{Q_i} \mathit{C_i}= Q_{in} \mathit{C_{in}}+A_s P \mathit{C_p}+A_s ET \mathit{C_{ET}}
where Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \mathit{Q_{in}C_{in}} is the input mass flow rate, Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \mathit{P C_p} is the precipitation loading rate, and Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \mathit{ET C_{ET}} is evapotranspiration mass flux.
As before the equations rearranged to form the dynamical system:
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): V_1 \frac{\partial \mathit{C_1}}{\partial t}= Q_i\left (\mathit{C_i} - \mathit{C_1} \right )+E'\left (\mathit{C_2} - \mathit{C_1} \right )
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): V_2 \frac{\partial \mathit{C_2}}{\partial t}= -E'\left (\mathit{C_2} - \mathit{C_1} \right )
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \frac{\partial A}{\partial t}=\mathit{C}- \frac {1}{\tau_c}\mathit{A} \qquad (7)
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): \mathit{Age}= {\alpha}(t) =\frac{\mathit{A}(t)}{\mathit{C}(t)},\quad
Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\tau_c}(t) =\frac{V(t)}{Q(t)}
where Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): V(t)= V_1 +V_2 is the total lake volume, Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): C(t) is concentration and Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): A(t) is 1st moment. The characteristic time in this case is not constant Failed to parse (Missing <code>texvc</code> executable. Please see math/README to configure.): {\tau_c}(t) and the equations are nonlinear which will require numerical solutions.
Reactions, Sources and Sinks
The effect of solute reactions on the reacting species concentration and age will be examined next. To demonstrate, a 2-component series reaction for unsteady flow is formulated.
0th order
1st order
multiple reactions
Lake-Catchment Dynamical System
To be written.