Difference between revisions of "Document PIHM manual calibration"

From Age of Water
Jump to: navigation, search
(Added PropertyValue: Expertise = calibration)
 
(10 intermediate revisions by 3 users not shown)
Line 5: Line 5:
 
==Parameters controlling lateral groundwater flow==
 
==Parameters controlling lateral groundwater flow==
  
−
Parameters controlling lateral groundwater flow include horizontal saturated hydraulic conductivity, KsatH, horizontal macropore hydraulic conductivity, MacKsatH, and macropore depth, MacD. [[File:Jepsen sample recession calib results.jpg|200px|thumb|right|FIGURE 1. Examples of of PIHM-modeled versus observed (from power law) streamflow recession.]] The soil thickness, to which groundwater flow is also sensitive, is held at an assumed value/distribution. Models are run forward in time from an initial state of completely saturated soil using all meteorological forcings (with precipitation set to zero) to capture the steepening effect of ET on the slope of the recession curve. RMS errors are minimized between modeled stream discharge (base flow) and observed values. The "observed" stream discharge is taken to be the time-dependent solution to the power law -dQ/dt = a*Q^b that best fits observation. Figure 1 (right) illustrates how the different parameters impact the shape of the modeled recession curve. The model calibration runs are executed using in-house Python scripts, and consist of all combinations of the above three parameters in 10 divisions (1000 runs per set). Generally two sets are carried out per calibration, yielding 2000 runs total per calibration.
+
Parameters controlling lateral groundwater flow include horizontal saturated hydraulic conductivity, KsatH, horizontal macropore hydraulic conductivity, MacKsatH, and macropore depth, MacD. [[File:Jepsen_sample_recession_calib_results.jpg|200px|thumb|right|FIGURE 1. Examples of of PIHM-modeled versus observed (from power law) streamflow recession.]] The soil thickness, to which groundwater flow is also sensitive, is held at an assumed value/distribution. Models are run forward in time from an initial state of completely saturated soil using all meteorological forcings (with precipitation set to zero) to capture the steepening effect of ET on the slope of the recession curve. RMS errors are minimized between modeled stream discharge (base flow) and observed values. The "observed" stream discharge is taken to be the time-dependent solution to the power law -dQ/dt = a*Q^b that best fits observation. Figure 1 (right) illustrates how the different parameters impact the shape of the modeled recession curve. The model calibration runs are executed using in-house Python scripts, and consist of all combinations of the above three parameters in 10 divisions (1000 runs per set). Generally two sets are carried out per calibration, yielding 2000 runs total per calibration.
  
 
==Parameters controlling infiltration==
 
==Parameters controlling infiltration==
Line 11: Line 11:
 
Methods presently under development.
 
Methods presently under development.
  
−
=Temperature index snow accumulation and melt model==
+
==Temperature index snow accumulation and melt model==
  
 
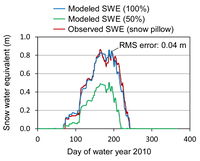
We are presently using a simple model of spatially uniform snow accumulation and melt within the 1 km^2 catchment of our study area. [[File:2010_UpperProv_SWEmodTindex.jpg|200px|thumb|right|FIGURE 2. Modeled snow water equivalent using a temperature-index model compared to observations at a nearby snow pillow.]] We may add spatial variability in snow accumulation and melt at a later stage in this analysis, depending on our later objectives. The model uses the temperature index method, described in Kumar (2009, p. 100), consisting of 4 parameters: 2 parameters controlling the partitioning of new precipitation between snowfall and rainfall [Ts and Tr (deg C)], a parameter controlling the air temperature at which melt begins, and a parameter controlling the increase in melt rate with air temperature (m day^-1 degC^-1). These parameters are determined in an external Excel spreadsheet using a routine, solved with the Solver add-in, that minimizes the RMS error between the time series of modeled and observed snow water equivalent (SWE) (snow pillow). We are able to separate out the snow model from PIHM this way because of the independence between snowmelt and hydrologic fluxes in the modeling framework. We generally obtain RMS errors ranging between 2 and 4 cm SWE (Figure 2). We incorporated into PIHM the accumulation parameters Tr and Ts as calibration parameters in order to fine tune our calibrations. Figure 2 shows model results for full modeled SWE (100%) and 50% modeled SWE, the latter produced by setting Tr and Ts to values of -4.4 deg C.
 
We are presently using a simple model of spatially uniform snow accumulation and melt within the 1 km^2 catchment of our study area. [[File:2010_UpperProv_SWEmodTindex.jpg|200px|thumb|right|FIGURE 2. Modeled snow water equivalent using a temperature-index model compared to observations at a nearby snow pillow.]] We may add spatial variability in snow accumulation and melt at a later stage in this analysis, depending on our later objectives. The model uses the temperature index method, described in Kumar (2009, p. 100), consisting of 4 parameters: 2 parameters controlling the partitioning of new precipitation between snowfall and rainfall [Ts and Tr (deg C)], a parameter controlling the air temperature at which melt begins, and a parameter controlling the increase in melt rate with air temperature (m day^-1 degC^-1). These parameters are determined in an external Excel spreadsheet using a routine, solved with the Solver add-in, that minimizes the RMS error between the time series of modeled and observed snow water equivalent (SWE) (snow pillow). We are able to separate out the snow model from PIHM this way because of the independence between snowmelt and hydrologic fluxes in the modeling framework. We generally obtain RMS errors ranging between 2 and 4 cm SWE (Figure 2). We incorporated into PIHM the accumulation parameters Tr and Ts as calibration parameters in order to fine tune our calibrations. Figure 2 shows model results for full modeled SWE (100%) and 50% modeled SWE, the latter produced by setting Tr and Ts to values of -4.4 deg C.
Line 23: Line 23:
 
<!-- Do NOT Edit below this Line -->
 
<!-- Do NOT Edit below this Line -->
 
{{#set:
 
{{#set:
−
  Led by=Tom_Harmon  |
+
Expertise=Calibration|
−
  Led by=Steve_Jepsen  }}
+
Owner=Chris_Duffy|
 +
Participants=Xuan_Yu|
 +
Progress=100|
 +
StartDate=2014-11-01|
 +
TargetDate=2015-11-01|
 +
Type=Low}}

Latest revision as of 13:58, 19 October 2015


"Manual calibration" of PIHM is a semi-automated procedure consisting of 3 steps: calibration of parameters controlling lateral groundwater flow, calibration of parameters controlling infiltration, and offline calibration of a simple temperature index model of snow accumulation and melt. These steps are summarized below.

Parameters controlling lateral groundwater flow

Parameters controlling lateral groundwater flow include horizontal saturated hydraulic conductivity, KsatH, horizontal macropore hydraulic conductivity, MacKsatH, and macropore depth, MacD.
FIGURE 1. Examples of of PIHM-modeled versus observed (from power law) streamflow recession.
The soil thickness, to which groundwater flow is also sensitive, is held at an assumed value/distribution. Models are run forward in time from an initial state of completely saturated soil using all meteorological forcings (with precipitation set to zero) to capture the steepening effect of ET on the slope of the recession curve. RMS errors are minimized between modeled stream discharge (base flow) and observed values. The "observed" stream discharge is taken to be the time-dependent solution to the power law -dQ/dt = a*Q^b that best fits observation. Figure 1 (right) illustrates how the different parameters impact the shape of the modeled recession curve. The model calibration runs are executed using in-house Python scripts, and consist of all combinations of the above three parameters in 10 divisions (1000 runs per set). Generally two sets are carried out per calibration, yielding 2000 runs total per calibration.

Parameters controlling infiltration

Methods presently under development.

Temperature index snow accumulation and melt model

We are presently using a simple model of spatially uniform snow accumulation and melt within the 1 km^2 catchment of our study area.
FIGURE 2. Modeled snow water equivalent using a temperature-index model compared to observations at a nearby snow pillow.
We may add spatial variability in snow accumulation and melt at a later stage in this analysis, depending on our later objectives. The model uses the temperature index method, described in Kumar (2009, p. 100), consisting of 4 parameters: 2 parameters controlling the partitioning of new precipitation between snowfall and rainfall [Ts and Tr (deg C)], a parameter controlling the air temperature at which melt begins, and a parameter controlling the increase in melt rate with air temperature (m day^-1 degC^-1). These parameters are determined in an external Excel spreadsheet using a routine, solved with the Solver add-in, that minimizes the RMS error between the time series of modeled and observed snow water equivalent (SWE) (snow pillow). We are able to separate out the snow model from PIHM this way because of the independence between snowmelt and hydrologic fluxes in the modeling framework. We generally obtain RMS errors ranging between 2 and 4 cm SWE (Figure 2). We incorporated into PIHM the accumulation parameters Tr and Ts as calibration parameters in order to fine tune our calibrations. Figure 2 shows model results for full modeled SWE (100%) and 50% modeled SWE, the latter produced by setting Tr and Ts to values of -4.4 deg C.

References

Kumar, M. (2009). Toward a hydrologic modeling system. Doctoral dissertation, The Pennsylvania State University, 273 p.


Yandex.Metrica
Retrieved from "https://www.organicdatascience.org/ageofwater/index.php?title=Document_PIHM_manual_calibration&oldid=10031"